

Ever wondered if there’s an easier way to find the limits of a function without their graph or table of values? We can use the different properties and laws of limits available. Limit laws are important in manipulating and evaluating the limits of functions.
Limit laws are helpful rules and properties we can use to evaluate a function’s limit.
Limit laws are also helpful in understanding how we can break down more complex expressions and functions to find their own limits. In this article, we’ll learn about the different limit laws and also discuss other limit properties that may help us in our next pre-calculus and calculus topics.
Before establishing these properties and learning how to apply them, why don’t we go ahead and begin with the definition of limit laws?
As we have mentioned, limit laws are the different laws or properties we can apply to manipulate functions and eventually find their limits.
For example, if we want to find the limit of $f(x) = -2x^2 + 5x – 8$ as it approaches 6, our previous knowledge would tell us to either graph or construct a table of values.
However, with the limit laws, we’ll need a few steps to evaluate $\lim-2x^2 + 5x – 8$.
Don’t worry. Once you’re introduced to a list of limit laws, evaluating limits will be easier for you as well! In fact, we have already learned some of these limit laws in the past – but they are in much simpler and general forms.
Note that throughout the entire discussion, we will assume that the two expressions, $ \lim_ f(x)$ and $ \lim_ g(x)$, exist and $a$ is a constant.
Why don’t we slowly introduce ourselves to the properties of limits and laws that may help us? This section will also explore examples that make use of these properties and laws, so we can better understand them as well.
If this is your first time encountering these properties, try to write down the limit laws’ names and algebraic definitions. Summarize these in one table as your guide for this section’s examples and the next topics you might encounter involving a function’s limit.
Don’t have a paper or your note-taking app nearby? No worries, we also summarized these properties for you at the end of this section!
We’ll group with these two basic laws of limits because they are the two most applied laws and the simplest laws of limits. These are constant and identity laws.
Constant Law: $\boldsymbol <\lim_
This limit law states that the limit of a constant $c$, as $x$ approaches $a$, is just equal to the constant itself.
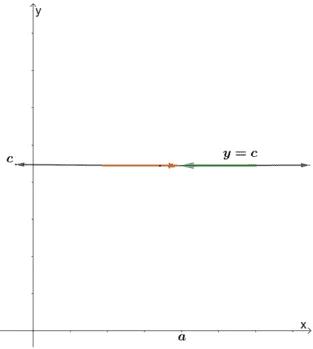
The graph above illustrates why the constant law is true for all values of $a$ and $c$. Regardless of the value of $a$, the function will continue to be equal to $c$.
Here are a few examples on how we can apply constant law for some limits.
Identity Law: $\boldsymbol <\lim_
Know why we call this the identity law? That’s because we’re dealing with the linear function, $y = x$, for this law of limit. The law of limit states that the limit of $ y = x$ as it approaches $a$ is equal to the number (or $a$) as $x$ approaches it.
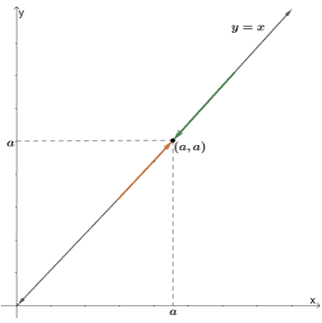
Here’s an illustration of why the identity law is true for all values of $x$. As $x$ approaches $a$, the value will of $y$ will depend on the value of $x$, so as $x$ approaches $a$, $y$ will also approach $a$.
Check out these three examples to better understand the identity law.
Ready to learn more limit laws? Here are five more that focus on the four arithmetic operations: addition, subtraction, multiplication, and division.
We’re grouping these limit laws because they share similar forms and contain the four most used arithmetic operations in a given function.
The addition law reiterates that when we take the limit of the sum of two functions, the result is equivalent to the sum of the respective limits of the function as $x$ approaches $a$.
If $\lim_ f(x) = -2$ and $\lim_ g(x) = 5$, this means that $ <\lim_
This law is similar to its addition counterpart. It states that the limit of two functions’ difference is just equal to the difference between the limits of each function as $x \rightarrow a$.
Why don’t we apply this law along with constant and identity laws to simplify $ \lim_ (x – 4 )$.
This is a good example showing how all these properties are applied in simplifying and evaluating limits.
Coefficient Law: $\boldsymbol <\lim_c \cdot f(x)= c \lim_ f(x)> $
This law states that the limit of the product shared by a constant, $c$, and the function, $f(x)$, will be the same when we multiply $c$ to the limit of $f(x)$ as it approaches $a$.
Here are some straightforward applications of this law:
Like addition and subtraction laws, this particular limit law states that the limit of the product of two functions is equal to the product of each function’s corresponding limits.
Why don’t we try to simplify $\lim_ 2x$ using the product law and the previous laws we’ve learned?
This means that the limit of the quotient of two functions is equivalent to the ratio of each of the functions’ limits. Note that this law is only applicable when $\lim_ g(x) \neq 0$.
This means that if $\lim_ f(x) = P$ and $\lim_ g(x) = Q$, the limit of $\dfrac$ as $x \rightarrow a$ is equal to $\dfrac <\lim_f(x)> <\lim_g(x)> = \dfrac$.
Now that we’ve covered all the limit laws that involve the four basic operations, it’s time to up our game and let’s learn about the limit laws for functions that contain exponents and roots.
Power Law: $\boldsymbol <\lim_[f(x)]^n = \left[\lim_ f(x) \right]^n>$, where $\boldsymbol <\lim_f(x) \neq 0>$ at $\boldsymbol$
The limit of the function that is raised to $n^$ power will return the same result when we find the limit of $f(x)$ first as $x$ approaches $a$ then raising the result by $n^$ power.
Note that this law is only true when the limit of $f(x)$ as $x$ approaches $a$ is not zero when $n$ is negative.
Simplifying $\lim_ (x – 1)^4$ will require us to use power law. Let’s go ahead and take a look at how we can simplify this expression.
Root Law: $\boldsymbol <\lim_\sqrt[n] = \sqrt[n] < \lim_f(x)>>$, where $\boldsymbol <\lim_f(x) \geq >$ where $\boldsymbol$ is even
Remember that $k^> = \sqrt[n]$, so the root law is actually an extension of the power law. This means that the limit of the $n^$ root of the function is also equal to the $n^$ root of the function’s limit as $x$ approaches $a$.
Since we have restrictions when the root is even, ensure that the limit of $f(x)$ as it approaches $a$ is positive when $n$ is even.
Let’s apply what we’ve just learned to simplify $\lim_ \sqrt[3]$ if $\lim_ f(x) = -27$?
Using the root law, we have $\lim_ \sqrt[3] = \sqrt[3] < \lim_f(x)> $. Given that $\lim_ f(x) = -27$, we now have $\lim_ \sqrt[3] = \sqrt[3] < -27>$ or $-3$.
Have you noticed a common pattern shared by all the limit laws we’ve just learned? The general rule shown by the limit laws is that whenever we apply an operation on a function’s limit, we can instead find the limit of the function first then take the limit of the resulting expression.
We’ll learn more about the applications of limit laws when we learn how to evaluate the limits of more complex functions. For now, let’s go ahead first and summarize the limit laws that we’ve just learned throughout this article.
| Limit Law | Algebraic Definition | Example |
| Constant Law | $ \lim_ c = c$ | $\lim_ 4 = 4 $ |
| Identity Law | $\lim_ x = a$ | $\lim_ x = 3 $ |
| Addition Law | $\lim_ [f(x) + g(x)] = \lim_ f(x) + \lim_ g(x) $ | $\lim_ [(x – 1)+ (2x)] = \lim_ (x – 1) + \lim_ 2x $ |
| Subtraction Law | $\lim_ [f(x) – g(x)] = \lim_ f(x) – \lim_ g(x) $ | $\lim_ [(x – 1) -(2x)] = \lim_ (x – 1) – \lim_ 2x $ |
| Coefficient Law | $\lim_ cf(x) = c \lim_ f(x) $ | $\lim_ \sqrt x = \sqrt \lim_ x $ |
| Product Law | $\lim_ [f(x) \cdot g(x)] = \lim_ f(x) \cdot \lim_ g(x) $ | $\lim_ [(x – 1) \cdot (2x)] = \lim_ (x – 1) \cdot \lim_ 2x $ |
| Quotient Law | $\lim_ \dfrac = \dfrac <\lim_f(x) > <\lim_g(x) >$ | $\lim_ \dfrac = \dfrac <\lim_x – 1 > <\lim_2x >$ |
| Power Law | $\lim_ [f(x)]^n = \left[\lim_ f(x) \right]^n $ | $\lim_ [2(x + 1)]^4 = \left[\lim_ 2(x + 1)\right]^4$ |
| Root Law | $\lim_ \sqrt[n] = \sqrt[n] < \lim_f(x)>$ | $\lim_ \sqrt[4] <2(x + 1)>= \sqrt[4] < \lim_2(x + 1)>$ |
Make sure to review all the properties we’ve discussed in the previous section before answering the problems that follow.
Example 1
Given that $\lim_ f(x) = -24$ and $\lim_ g(x) = 4$, find the value of the following expressions using the properties of limits we’ve just learned.
When working with problems like these for the first time, it’s always helpful to have a list of the limit laws we’ve just discussed. This way, you can always check for a limit law that may apply to our problem.
We can rewrite $\lim_ [f(x) + g(x)]$ as $\lim_ f(x) + \lim_ g(x) $ using the addition law.
Substitute the given values for the limits of $f(x)$ and $g(x)$ as they approach $a$.
a. This means that $\lim_ [f(x) + g(x)] = \boldsymbol$.
Similarly, we can rewrite $\lim_ [4 g(x)]$ as $4\lim_ g(x)$ using the coefficient law.
b. Hence, $\lim_ [4 g(x)]$ is equal to $\boldsymbol$.
The third expression will require multiple limit laws before we can find the expression’s value. In fact, for this item, we’ll need the following properties:
Let’s go ahead and break down $\lim_ \dfrac>$ to see how these laws would be helpful for this item.
Using the final expression, let’s substitute $\lim_ f(x) = -24$ and $\lim_ g(x) = 4$ into the rational expression.
Example 2
Use the different properties of limits to find the values of the following expressions.
a. $\lim_ x^2 – 2x +1 $
b. $\lim_ ax^2 +bx + c$, where $a$, $b$, and $c$ are nonzero constants
What can you observe from the results? In general, how can we evaluate the limits of a quadratic function?
Apply the addition law on the expression, $\lim_ x^2 – 2x +1 $.
Simplify this further by applying the following limit laws on each of the terms:
| $\begin\lim_ x^2 &= \left(\lim_ x\right)^2\\&=(2)^2\end$ | $\begin\lim_ 2x &= 2\lim_ x\\&=2(2)\end$ | $\begin\lim_ 1 &= 1\end$ |
| $\begin\lim_ x^2 – 2x +1 &= (2)^2 -2(2)+1\\&= 4 – 4+1\\&=1\end$ | ||
a. This means that $\lim_ x^2 – 2x +1$ is equal to $\boldsymbol$.
Since we’re working with an expression that has a similar, we’ll also be using similar steps and the same limit laws to simplify $\lim_ ax^2 +bx + c$.
Using addition law, we’ll have $\lim_ ax^2 +bx + c = \lim_ ax^2 + \lim_ bx + \lim_ c$.
Let’s simplify each term and keep in mind that $a$, $b$, and $c$ are nonzero constants.
| $\begin\lim_ ax^2 &=a\lim_ x^2\\&=a\left(\lim_ x\right)^2\\&=a(k)^2\end$ | $\begin\lim_ bx &= b\lim_ x\\&=b(k) \end$ | $\begin\lim_ c &= c\end$ |
| $\begin\lim_ ax^2 +bx + c &=\lim_ ax^2 + \lim_ bx + \lim_ c\\&= \lim_ a(k)^2 – b(k) +c \end$ | ||
b. Hence, the limit of $ax^2 + bx +c$ as $x$ approaches $k$ is $\boldsymbol$.
From the results of a and b, we have:
We can see that for each case, the resulting limits were equivalent to us finding the value of the given expression at $x = 2$ and $x = k$, respectively.
Since $ ax^2 + bx + c$ is the general form of quadratic expressions and $k$ can be any nonzero constant, this observation applies to all quadratic functions.
Meaning, when given a quadratic function, its limit as $\boldsymbol$ approaches $\boldsymbol$ can be determined by finding the value of the function at $\boldsymbol$.
Want a sneak peek at the next concepts you’ll learn on limits? In general, the limit of a polynomial function as it approaches $a$ is equal to the value of the function at $x = a$.
Example 3
By checking the expression, we can see that we’ll need several limit laws to find the expression’s value.
Start by working on the radical expression and apply the root law.
Apply the subtraction law to separate the two terms inside the cube root.
Let’s focus on the limit of the first term inside the cube root, $ \lim_ f(x)[g(x)]^2-\dfrac $, and find its numerical value by applying the following limit laws:
Now, let’s find the numerical value of $ \lim_\dfrac$ by applying the following limit laws.
Let’s substitute the values, $ \lim_ f(x)[g(x)]^2-\dfrac = 16$ and $ \lim_\dfrac = \dfrac$, into our original expression.
Example 4
Use the limit laws to find the value of $ \lim_ f(h)$ given that $f(h) = \dfrac + 8>$.
Since $f(x)$ contains a rational expression, we can apply the quotient law to apply the limit laws on both the numerator and denominator.
Simplify the denominator first by using the following limit laws:
Now that we have a numerical value for the denominator let’s go ahead and simplify the expression.
Simplify this expression by applying the following properties:
This means that $ \lim_\dfrac + 8>$ is equal to $\boldsymbol – 8 >$.
Having fun with the process of finding the limits using the different properties? Guess what? You’ll actually learn more properties and techniques in evaluating limits in this article!
For now, we’ve provided more problems for you to try on your own to master these limit laws.